已知{an}是公比为q的等比数列，且am、am+2、am+1成等差数列．（1）

问题解答题

已知{a_n}是公比为q的等比数列，且a_m、a_m+2、a_m+1成等差数列．

（1）求q的值；

（2）设数列{a_n}的前n项和为S_n，试判断S_m、S_m+2、S_m+1是否成等差数列？并说明理由．

答案

（1）q＝1或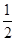－．（2）当q＝1时，S_m , S_m+2 , S_m+1不成等差数列；q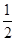＝－时，S_m , S_m+2 , S_m+1成等差数列．

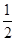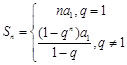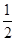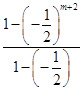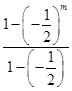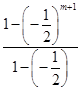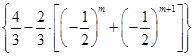题目分析：（1）根据三数成等差数列，列出等量关系：2a_m+2＝a_m+1＋a_m∴2a₁q^m+1＝a₁q^m＋a₁q^{m – 1}^，在等比数列{a_n}中，a₁≠0，q≠0，∴2q²＝q＋1，解得q＝1或－．（2）根据等比数列前n项和公式分类讨论：若q＝1，S_m＋S_m+1＝ma₁＋(m＋1)a₁＝(2m＋1)a₁，S_m+2＝(m＋2)a₁∵a₁≠0，∴2S_m+2≠S_m＋S_m+1若q＝－，S_m+2＝·a₁＝·a₁，S_m＋S_m+1＝·a₁＋·a₁＝·a₁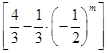＝·a₁_，∴2 S_m+2＝S_m＋S_m+1

解：（1）依题意，得2a_m+2＝a_m+1＋a_m∴2a₁q^m+1＝a₁q^m＋a₁q^{m – 1}

在等比数列{a_n}中，a₁≠0，q≠0，∴2q²＝q＋1，解得q＝1或－．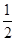

（2）若q＝1，S_m＋S_m+1＝ma₁＋(m＋1)a₁＝(2m＋1)a₁，S_m+2＝(m＋2)a₁

∵a₁≠0，∴2S_m+2≠S_m＋S_m+1

若q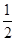＝－，S_m+2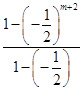＝·a₁＝·a₁

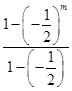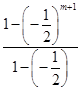S_m＋S_m+1＝·a₁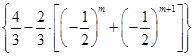＋·a₁＝·a₁

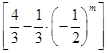＝·a₁ ∴2 S_m+2＝S_m＋S_m+1

故当q＝1时，S_m , S_m+2 , S_m+1不成等差数列；q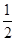＝－时，S_m , S_m+2 , S_m+1成等差数列．