问题
选择题
(2014·孝感模拟)已知函数f(x)是R上的单调增函数且为奇函数,数列{an}是等差数列,a3>0,则f(a1)+f(a3)+f(a5)的值( )
A．恒为正数
B．恒为负数
C．恒为0
D．可以为正数也可以为负数
答案
答案：A
因为函数f(x)是R上的奇函数,所以f(-0)=-f(0)⇒f(0)=0,又f(x)是R上的增函数,所以当x>0时有f(x)>f(0)=0,当x<0时有f(x)<f(0)=0,因为a3>0,所以有f(a3)>0,
因为数列{an}是等差数列,所以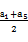
=a3>0⇒a1+a5>0⇒a1>-a5⇒f(a1)>f(-a5),又f(-a5)=-f(a5),所以f(a1)+f(a5)>0,即有f(a1)+f(a3)+f(a5)
=[f(a1)+f(a5)]+f(a3)>0.