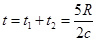问题
计算题
（1）（6分）如图所示，同种介质中有两列简谐横波相向传播，实线表示的波向x轴正方向传播，虚线表示的波向x轴负方向传播，在t=0时刻，两列波已在2m≤x≤4m范围内相遇。已知波的频率为5Hz，两列波的振幅均为lcm，则波的传播速度为 m/s；两列波相遇后，x=3m处质点的振幅为 cm。
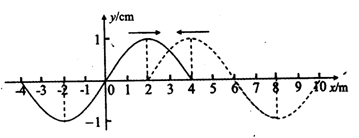
（2）（9分）如图所示，一玻璃砖的横截面为半圆形，O为圆心，半径为R，MN为直径，P为OM的中点，MN与水平放置的足够大光屏平行，两者间距为d=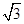
R。一单色细光束沿垂直于玻璃砖上表面的方向从P点射入玻璃砖，光从弧形表面上A点射出后到达光屏上Q点。已知玻璃砖对该光的折射率为n=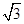，求光束从P点到达Q点所用的时间（不考虑反射光，光在真空中传播速度为c）。
答案
(1)40 2 (2)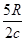
题目分析：(1)两列波在同一介质中传播，波速相同，根据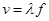
得，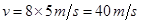
．波发生叠加时，质点参与了两列波的振动，根据对称性，两列波的波峰或波谷同时传到x=3m处质点，该质点振动始终加强，根据叠加原理，振幅等于两列波振幅之和，即A=1cm+1cm=2cm．
(2)根据题设做出光路图如图所示
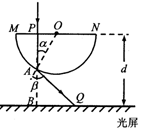
设出射点处的入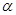射角为
，折射角为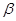
．由几何关系知：
， ①
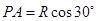②
设光在玻璃砖中的传播速度为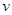
，传播时间为
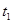，则
③
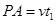④
联立①②③④解得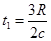 
由折射定律得：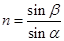
⑤
由几何关系知，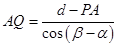
⑥
设光从A到Q所用时间为
，则
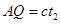⑦
联立①②⑤⑥⑦解得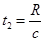 
因此从P到Q的时间为