问题
解答题
已知函数f（x）是定义在[﹣1，1]上的奇函数，当x∈[0，1]时，f（x）=2x+ln（x+1）﹣1．
（1）求函数f（x）的解析式；并判断f（x）在[﹣1，1]上的单调性（不要求证明）；
（2）解不等式f（2x﹣1）+f（1﹣x2）≥0．
答案
解：（1）设﹣1≤x≤0，则0≤﹣x≤1，
所以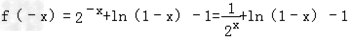
．
又f（x）是奇函数，
所以f（﹣x）=﹣f（x），
于是f（x）=﹣f（﹣x）=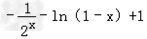
．
故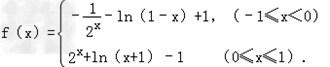
判断：f（x）在[﹣1，1]上是增函数；
（2）因奇函数f（x）在[﹣1，1]上是增函数，
所以f（2x﹣1）+f（1﹣x2）≥0
f（2x﹣1）≥f（x2﹣1）
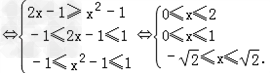
解得0≤x≤1，
所以不等式的解集为{x|0≤x≤1}．