问题
解答题
已知二次函数f（x）=ax2+bx+c（a≠0）的图象过点（0，1），且与x轴有唯一的交点（﹣1，0）．
（Ⅰ）求f（x）的表达式；
（Ⅱ）设函数F（x）=f（x）﹣kx，x∈[﹣2，2]，记此函数的最小值为g（k），求g（k）的解析式．
答案
解：（Ⅰ）∵二次函数f（x）=ax2+bx+c（a≠0）的图象过点（0，1），且与x轴有唯一的交点（﹣1，0）．
∴c=1，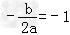
，b2﹣4ac=0
解得a=1，b=2，c=1，
从而f（x）=x2+2x+1；
（Ⅱ）F（x）=x2+（2﹣k）x+1，对称轴为
，图象开口向上
当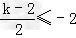
即k≤﹣2时，F（x）在[﹣2，2]上单调递增，
此时函数F（x）的最小值g（k）=F（﹣2）=2k+1
当
即﹣2＜k≤6时，F（x）在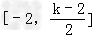
上递减，在
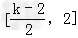上递增
此时函数F（x）的最小值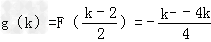
；
当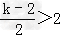
即k＞6时，F（x）在[﹣2，2]上单调递减，
此时函数F（x）的最小值g（k）=F（2）=9﹣2k；
综上，函数F（x）的最小值g（k）=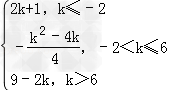
．