问题
解答题
已知函数f(x)是奇函数,其定义域为(﹣1,1),且在[0,1)上是增函数,若f(a﹣2)+f(3﹣2a)<0,试求a的取值范围.
答案
解:函数f(x)是奇函数,且在[0,1)上是增函数,
则f(x)在(﹣1,0]也是增函数,即f(x)在(﹣1,1)是增函数,
f(a﹣2)+f(3﹣2a)<0
∴f(a﹣2)<﹣f(3﹣2a)
∴f(a﹣2)<f(2a﹣3),
又由f(x)在(﹣1,1)是增函数,
则有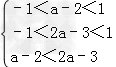 ,
,
解可得1<a<2,
故a的取值范围是1<a<2.
