解：（Ⅰ）当a=2时，f（x）= ，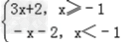

所以f（x）的单调递增区间是[﹣1，+∞），

因为f（x）在[b，+∞）上为增函数，

所以[b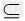，+∞）[﹣1，+∞），

故b≥﹣1

（Ⅱ）化简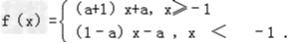 

①﹣1＜a＜1时，

当x≥﹣1时，f（x）=（a+1）x+a是增函数，且f（x）≥f（﹣1）=﹣1；

当x＜﹣1时，f（x）=（1﹣a）x﹣a是增函数，且f（x）＜f（﹣1）=﹣1．

所以，当﹣1＜a＜1时，函数f （x） 在R上是增函数．

②a=1或﹣1时，易知不合题意．

③当a＞1时，f（x）在[﹣1，+∞）为增函数，而在（﹣∞，﹣1）上为减函数，

故函数f（x）在R上不具有单调性；

同理，当a＜1时，函数f（x）在R上也不具有单调性．

综上可知，a的取值范围是 （﹣1，1）