问题
探究题
（1）A、B为同一波源发出的两列波，某时刻在不同介质、相同距离上的波形如图所示，则两列波的波速之比vA：vB是______________；
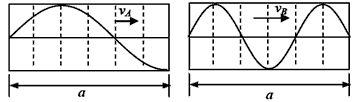
A．1：3
B．1：2
C．2：1
D．3：1
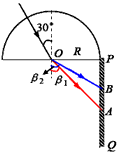
（2）如图所示，半圆形玻璃砖的半径为R，光屏PQ置于直径的右端并与直径垂直，一复色光与竖直方向成α=30°角射入玻璃砖的圆心O，由于复色光中含有两种单色光，故在光屏上出现了两个光斑，玻璃对两种单色光的折射率分别为n1=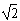
和n2=
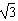，求：
①这两个光斑之间的距离；
②为使光屏上的光斑消失，复色光的入射角至少为多少？
答案
（1）C
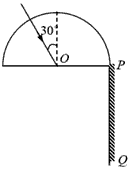
（2）①作出光路图如图
由折射定律有：n1=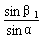
，n2=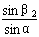
代入数据得：β1=45°，β2=60°
故有AB=PA－PB=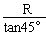
－
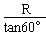=(1－
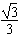)R
②当两种色光在界面处均发生全反射时光斑消失，随入射角α增大，玻璃对折射率为n2的色光先发生全反射，后对折射率为n1的色光发生全反射
故sinC=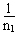
=
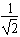
所以α=C=45°