问题
单项选择题
设A是n阶矩阵,且Ak=O(尼为正整数),则()。
A.A一定是零矩阵
B.A有不为0的特征值
C.A的特征值全为0
D.A有n个线性无关的特征向量
答案
参考答案:C
解析:
设A是A的特征值,.对应的特征向量为α,则有
Aα=λα Akα=λkα=0
由α≠0,有λk=0,即λ=0,故A的特征值全为0。
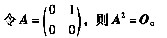
若A有n个线性无关的特征向量,则A可对角化,即存在可逆矩阵P,使得P-1AP=O,则必有A=O,与题意矛盾。
