问题
单项选择题
齐次线性方程组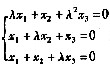 的系数矩阵记为A。若存在三阶矩阵B≠O使得AB=O,则()。
的系数矩阵记为A。若存在三阶矩阵B≠O使得AB=O,则()。
A.λ=-2且|B|=0
B.λ=-2且|B|≠0
C.λ=1且|B|=0
D.λ=1且|B|≠0
答案
参考答案:C
解析:
由题设条件:AB=O,且B≠0知方程组Ax=0存在非零解,于是|A|=0,即
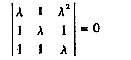
解得λ=1。
于是
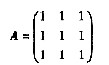
由AB=O,知BTAT=O。
故方程组BTx=0存在非零解,于是|B|=|BT|=0。
[解析2]因为AB=O,所以r(A)+r(B)≤3,
又A≠O,B≠O,
所以1≤r(A)<3,1≤r(B)<3,
故 |B|=0。

