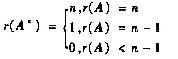问题
单项选择题
设三阶矩阵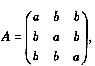
若A的伴随矩阵的秩等于1，则必有（）。
A．a=b或a+2b=0
B．a=b或a+2b≠0
C．a≠b且a+2b=0
D．a≠6且a+2b≠0
答案
参考答案：C
解析：
A的伴随矩阵的秩为1，说明A的秩为2，由此可确定a，b应满足的条件。根据A与其伴随矩阵A*秩之间的关系知，r(A)=2，故有
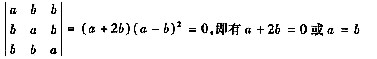
但当a=b时，显然r(A)≠2，故必有a≠b且a+2b=0，应选C。
[评注] n(n≥2)阶矩阵A与其伴随矩阵A*的秩之间有下列关系：
