问题
单项选择题
假设总体X～N(μ，1)，关于总体X的数学期望μ有两个假设：H0：μ=0，H1：μ=1设X1，X2，…，X9是来自总体X的简单随机样本，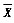
是样本均值，以μp表示标准正态分布水平p双侧分位数；则在H0的4个水平α=0.05的否定域中，第二类错误概率最小的否定域是()。
A.A
B.B
C.C
D.D
答案
参考答案：C
解析：
首先注意到4个否定域中，第一类错误概率都等于0.05。
解该题首先要靠直观“判断力”：因为统计量
反映数学期望μ与μ0=0的差异，当统计量
的值大到一定程度时，否定H0:μ:0，接受H1:μ=1，因此应选择C。
其实，如果计算各否定域的第二类错误概率，则可以得到同样结沦。事实上，由于在H1:μ=1成立的条件下
可见否定域Vk(k=1，2，3，4)的第二类错误概率为
利用正态分布函数数值表，可得：β1=0.14917，β2=0.999441，β3=0.0877，β4=0.999998。
可见以
为否定域的检验的第二类错误概率最小。