问题
单项选择题
设A，B为n阶矩阵，A*，B*分别为A，B对应的伴随矩阵，分块矩阵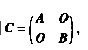
则C的伴随矩阵C*=()。
A.A
B.B
C.C
D.D
答案
参考答案：D
解析：
若A、B可逆，则C可逆，且C*=|C|·C-1，可求得C*。若A、B不全可逆，则对四个选项验证：C·C*=|C|E。
若A、B均可逆，则A*=|A|A-1，B*=|B|B-1，
从而
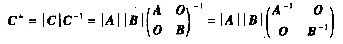
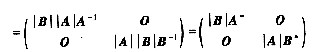
对比四个选项知，只有D成立。
当A或B不可逆时，利用定义可证D仍成立。