下列矩阵中不能对角化的是()。

A.A
B.B
C.C
D.D
参考答案:C
解析:
A项,
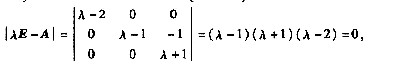
故A有三个不同的特征值,显然A可对角化。
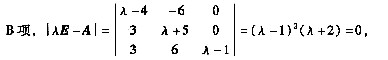
即特征值为λ1=1(二重),λ2=-2。
当λ=1时,r(E-A)=1,故λ=1对应两个线性无关的特征向量,故A可对角化。
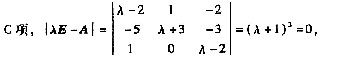
故λ=-1是三重特征值,而r(-E-A)=2,敞A不可对角化。
D项为实对称矩阵,它必町对角化。
下列矩阵中不能对角化的是()。

A.A
B.B
C.C
D.D
参考答案:C
解析:
A项,
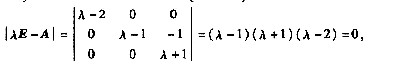
故A有三个不同的特征值,显然A可对角化。
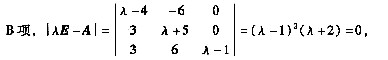
即特征值为λ1=1(二重),λ2=-2。
当λ=1时,r(E-A)=1,故λ=1对应两个线性无关的特征向量,故A可对角化。
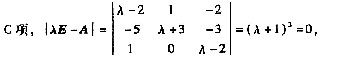
故λ=-1是三重特征值,而r(-E-A)=2,敞A不可对角化。
D项为实对称矩阵,它必町对角化。