问题
单项选择题
设曲线y=y（x）上点P（0，4）处的切线垂直于直线x-2y+5=0，且该点满足微分方程y"+2y'+y=0，则此曲线方程为（）。
A.A
B.B
C.C
D.D
答案
参考答案：D
解析：
y"+2y'+y=0(二阶常系数线性齐次方程)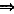
y=e-x(C1x+C2)(通解)。
由题意知y(0)=4，y'(0)=-2，于是可得C2=4，C1=2，
故y=e-x(2x+4)，即y=2(x+2)e-x。
搜索