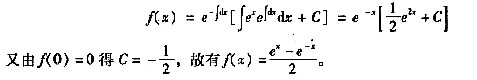问题
单项选择题
设曲线积分∫t[f（x）-ex]sinydx-f（x）cos）ydy与路径无关，其中f（x）具有一阶连续导数，且f（0）=0，则f（x）等于（）。
A.A
B.B
C.C
D.D
答案
参考答案：B
解析：
曲线积分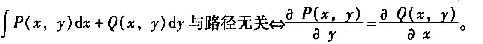
P(x，y)=[f(x)-ex]siny，Q(x，y)=-f(x)cosy，则由题设有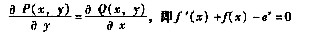
由一阶微分方程通解公式知
搜题请搜索小程序“爱下问搜题”
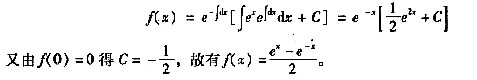
设曲线积分∫t[f（x）-ex]sinydx-f（x）cos）ydy与路径无关，其中f（x）具有一阶连续导数，且f（0）=0，则f（x）等于（）。
A.A
B.B
C.C
D.D
参考答案：B
解析：
曲线积分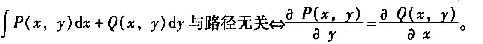
P(x，y)=[f(x)-ex]siny，Q(x，y)=-f(x)cosy，则由题设有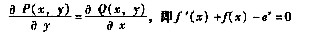
由一阶微分方程通解公式知