问题
单项选择题
已知曲面z=4-x2-y2上点P处的切平面平行于平面2x+2y+z-1=0,则点P的坐标是()。
A.(1,-1,2)
B.(-1,1,2)
C.(1,1,2)
D.(-1,-1,2)
答案
参考答案:C
解析:
先求出曲面在点P处切平面的法矢量,再由其与已知平面的法矢量对应元素成比例,即可求出P的坐标。
设P点的坐标为(x0,y0,z0),则曲而在P点的切平面的法矢量为
n={-2x0,-2y0,-1}
又由切平面平行于平面2z+2y+z-1=0,因此有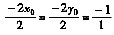
解得x0=1,y0=1,代入曲面方程解得z0=2。因此P点的坐标为(1,1,2)。
