问题
单项选择题
设函数f(x)在x=a的某个邻域内连续,且f(a)为其极大值,则存在δ>0,当x∈(a-δ,a+δ)时,必有()。

A.A
B.B
C.C
D.D
答案
参考答案:C
解析:
利用极大值的定义讨论即可。
由题设,存在邻域(a-δ,a+δ),使当x∈(a-δ,a+δ)时,有f(x)≤f(a),所以
当a-δ<x<a时,(x-a)[f(x)-f(a)]≥0;
当a<x<a+δ时,(x-a)[f(x)-f(a)]≤0。
因此AB两项不成立。
考虑到CD两项中分母均大于零,而分子部分有
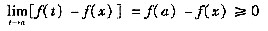
所以必有C项成立。
