问题
单项选择题
下列各点中为二元函数z=x3-y3-3x2+3y-9x的极值点的是()。
A.(3,-1)
B.(3,1)
C.(1,1)
D.(-1,-1)
答案
参考答案:A
解析:
由方程组
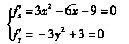
得f的稳定点为P0(-1,-1),P1(-1,1),P2(3,-1),P3(3,1)。
而由A=f"xx=6x-6,B=f"xy=0,C=f"yy=-6y可得:
在P0(-1,-1)处,由A=-12<0,B=0,C=6,AC-B2=-72<0可得,f不能取得极值;
在P1(-1,1)处,由A=-12<0,B=0,C=-6,AC-B2=72>0可得,f取得极大值;
在P2(3,-1)处,由A=12>0,B=0,C=6,AC-B2=72>0可得,f取得极小值;
在P3(3,1)处,由A=12>0,B=0,C=-6,AC-B2=-72<0可得,f不能取得极值;
