小李在一旅游景区附近租下一个小店面卖纪念品和T恤,由于经营条件限制,他最多进50件T恤和30件纪念品,他至少需要T恤和纪念品40件才能维持经营,已知进货价为T恤每件36元,纪念品每件50元,现在他有2400元可进货,假设每件T恤的利润是18元,每件纪念品的利润是20元,问怎样进货才能使他的利润最大,最大利润为多少?
设进T恤x件,纪念品y件,可得利润为z元,由题意得x、y满足的约束条件为:
,且x、y∈N* 0≤x≤50 0≤y≤30 x+y≥40 36x+48y≤2400
目标函数z=18x+20y
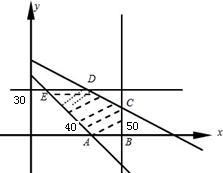
约束条件的可行域如图所示:
五边形ABCDE的各个顶点坐标分别为:A(40,0),B(50,0),
C(50,
),D(25 2
,30),E(10,30),80 3
当直线l:z=18x+20y经过C(50,
)时取最大值,25 2
∵x,y必为整数,∴当x=50,y=12时,z取最大值
即进50件T恤,12件纪念品时,可获最大利润,最大利润为1140元.

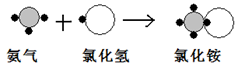
 ”表示氢原子,用“
”表示氢原子,用“ ”表示氮原子,用“
”表示氮原子,用“ ”表示氯原子,上述反应过程可用下图表示:
”表示氯原子,上述反应过程可用下图表示: