问题
解答题
| 关于x的一元二次方程x2-2x-m=0 ①已知1+
②判断命题:“若m≤2,则方程x2-2x-m=0总有两个不相等的实数根”的真假,如果是真命题请给出证明;如果是假命题请举出一个反例说明 |
答案
①设方程的另一个根为x1,则:
x1+1+
=2,3
∴x1=1-
.3
x1•(1+
)=-m,3
(1-
)(1+3
)=-2=-m,3
∴m=2.
故另一个根是:1-
,m=2.3
②△=4+4m>0,
m>-1.
∴当m>-1时,方程总有两个不等实数根.
故命题“若m≤2,则方程x2-2x-m=0总有两个不相等的实数根”是假命题.
如当m=-2时,方程为x2-2x+2=0,此时△=4-8=-4<0,方程没有实数根.

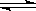 XC(g)符合如图像(Ⅰ)所示关系。由此推断对图(Ⅱ)的正确说法是( )
XC(g)符合如图像(Ⅰ)所示关系。由此推断对图(Ⅱ)的正确说法是( )