问题
单项选择题
设随机变量X在区间(0,1)上服从均匀分布,又
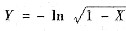 ,求Y的概率密度fY(y)与分布函数FY(y).
,求Y的概率密度fY(y)与分布函数FY(y).
答案
参考答案:[解法一] 应用单调函数公式法先求Y的概率密度fY(y):
由于X在(0,1)内取值.因此[*]的值域为(0,+∞),而且函数y=g(x)在(0,1)内单调.其反函数x=1-e-2y[*]h(y)在(0,+∞)内单调可导,其导数h'(y)=2e-2y在其定义域(0,+∞)内恒不为零·又因X的概率密度[*]故Y的概率密度为
[*]
可见,Y是服从参数为2的指数分布,其分布函数为
[*]
[解法二] 用分布函数法先求出Y的分布函数:
当y≤0时,FY(y)≤0;
当y>0时,0<x=1-e-2y<1,
[*]
最后一步是由于X服从(0,1)上均匀分布,其分布函数当0<1-e2y<1时,FX(1-e-2y)=1-e-2y,所求Y的分布函数为
[*]
将FY(y)对y求导数,得到Y的概率密度为
[*]
解析:
[*]
