问题
单项选择题
设总体X服从自由度为m的χ2分布，其概率密度是f(x；m)．X1，X2，…，Xn是取自X的一个简单随机样本，其样本均值
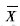的概率密度记为g(y)．(Ⅰ)试将g(y)用X的概率密度表示出来；(Ⅱ)具体计算Y的期望与方差．
答案
参考答案：[解] (Ⅰ) 根据简单随机样本的性质，X1，X2，…，Xn相互独立且与总体X同分布，即Xi～χ2(m)，i=1，2，…，n．应用χ2分布可加性可知
[*]
Y的概率密度为f(y，mn)．
[*]
(Ⅱ) 设随机变量Y1，Y2，…，Ymn相互独立且都服从标准正态分布N(0，1)，则随机变量[*]，…，Y2mn也相互独立且都服从一个自由度的χ2分布．于是
[*]
解析：
[*]