问题
单项选择题
设总体X的概率密度为
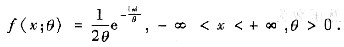
X1,X2,…,Xn是取自总体X的简单随机样本.求θ的矩估计量与最大似然估计量.
答案
参考答案:[解] 总体X的概率密度中只有一个未知参数,在求θ的矩估计量时我们首先考察X的期望,但是f(x)是一个偶函数,其数学期望为零.无法得到θ与EX的关系进行θ的矩估计,为此我们应该计算X的二阶原点矩EX2:
[*]
注意到被积函数中[*]是参数为[*]的指数分布,因此积分[*]可以看作是参数为[*]的指数分布的随机变量Y的二阶原点矩,其值为
EY2=DY+(EY2)=θ2+θ2=2θ2.
又[*]
于是θ的矩估量为[*]
设x1,x2,…,xn是样本X1,X2,…,Xn的观测值,似然函数为
[*]
解上述方程得θ的最大似然估计值为[*],因此θ的最大似然估计量为[*]
