问题
单项选择题
随机变量序列X1,…,Xn,…相互独立且满足大数定律,则Xi的分布可以是
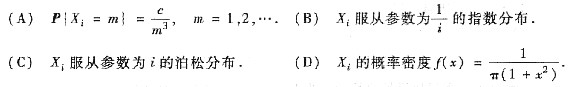
答案
参考答案:A
解析:
[分析]: 相互独立的随机变量X1,X2,…,如果X1,X2,…同分布,只要EXi存在,则X1,X2,…服从辛钦大数定律;若X1,X2,…不同分布,但Xi的期望、方差应都存在,且方差要一致有界,则X1,X2,…满足切比雪夫大数定律.据此分析:
在(A)中,Xi同分布,[*],由于级数[*]是收敛的,因此EXi存在,X1,X2,…满足辛钦大数定律,应选(A).
进一步分析,在(B)中,[*];在(c)中,DXi=i,它们均不能对i一致有界,因此不满足切比雪夫大数定律.
在(D)中,由于[*],因此[*].故EXi不存在,所以不能满足辛钦大数守律.
