搜题请搜索小程序“爱下问搜题”
问题 单项选择题

设二维随机变量(X，Y)在矩形区域D=(x，y)：0≤x≤2，0≤y≤1上服从二维均匀分布，随机变量


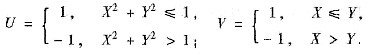
(Ⅰ) 求U和V的联合概率分布；
(Ⅱ) 讨论U和V的相关性与独立性．

答案

参考答案：[解] 依题意可知X与Y的联合概率密度为
[*]
(Ⅰ) (U，V)的可能取值为(-1，-1)，(-1，1)，(1，-1)，(1，1)，如图10-1，则有
[*]
[*]
类似地可以计算出其他pij的值，列表如下：
[*]
(Ⅱ) 从(U，V)的联合分布与边缘分布可以计算出
EU=π/4-1，EV=-1/2，EUV=1/2．
计算可知 EUV≠EUEV，即U与V相关，当然U与V也一定不独立．

单项选择题

在哪些牙列缺损情况，需用间接固位体

A．前牙缺失
B．多数后牙缺失
C．末端游离缺失
D．多数前后牙缺失
E．间隔缺失
查看答案
单项选择题

2006年国家加大了对房地产市场的宏观调控，2006年全国房地产开发完成投资19382亿元，比去年同期增长21.8%。
2006年12月，全国70个大中城市房屋销售价格同比上涨5.4%，涨幅比上月高0.2个百分点，环比上涨0.6%，涨幅比上月高0.1个百分点，其中：
(一)商品住房销售价格同比上涨6.3%，涨幅比上月高0.5个百分点，环比上涨0.6%，涨幅与上月持平，分地区看，与去年同月比，涨幅较大的主要城市包括：秦皇岛11.8%，北京10.4%，深圳10.0%，福州9.8%，厦门9.1%，成都8.5%和广州83%等，上海微降0.1%，与上月比，涨幅超过1%的城市有16个，多数集中在中西部地区，主要包括：乌鲁木齐2.9%，南昌1.5%，昆明 1.4%，福州和兰州均为1%等。下降的城市有7个，主要包括：长沙1.7%，长春0.9%等。
(二)二手住房销售价格同比上涨4.2%，涨幅比上月低1个百分点，环比上涨0.7%，涨幅比上月低0.1个百分点，与去年同月比，涨幅最高的主要城市包括：郑州12.4%，深圳11.4%，大连 10.5%，北京10.3%，长沙8.9%和南昌8.7%等，与上月比，涨幅超过1%的城市有24个，主要包括：郑州3.3%，长沙3.2%，南昌2.2%，成都1.6%，乌鲁木齐1.4%，北京1.4%，福州和重庆均为 1.2%，厦门1.1%等，下降城市有8个，主要包括：海口2.5%，包头1.1%，大连0.5%，呼和浩特 0.4%，上海和兰州均为0.3%，长春0.2%等。(注：同比以去年同月价格为10，环比以上月价格为100)

2005年全国房地产开发完成投资()

A．19382亿元
B．4225亿元
C．15913亿元
D．3469亿元
查看答案