问题
单项选择题
设总体X服从[0,θ]上的均匀分布,X1,…,Xn是取自总体X的一个简单随机样本.
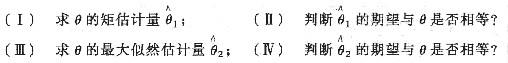
答案
参考答案:[解] (Ⅰ) 记EX=μ,则μ=EX=θ/2,即θ=2μ.故θ的矩估计量[*].
(Ⅱ) [*].
(Ⅲ) 对于总体X的样本值x1,…,xn,似然函数[*]
当θ<max(x1,…,xn)时,L=0;当θ≥max(x1,…,xn),[*]是θ的单调减函数,因此当θ=max(x1,…,xn)时,L达到最大值.故θ的最大似然估计量[*].
(Ⅳ) 为求[*]的期望值,需先求[*]的分布.
因总体X服从[0,θ]上均匀分布,因此Xi(i=1,…,n)都服从[0,θ]上均匀分布,其分布函数为
[*]
[*]的分布函数记为G(x),概率密度记为g(x),则
当x<0时,G(x)=0;当x>θ时,G(x)=1;当0≤x≤θ时,
[*]
由于X1,…,Xn相互独立,于是有
[*]
从而
[*]
