问题
单项选择题
设连续型随机变量X的分布函数为

求使得
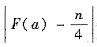 达到最小的正整数n.
达到最小的正整数n.
答案
参考答案:[解] 由于连续型随机变量X的分布函数是连续函数,因此F(x)在(-∞,+∞)内连续,当然在x=-1与x=1处也连续,于是有
[*]
解以a,b为未知量的二元一次方程组,可得[*]
当-1≤x<1时,
[*]
由于[*],且只有当[*]时为0,[*]时大于0.比较n=2与n=3的两个值:
当n=2时,[*]
当n=3时,[*]
因此可知,当n=3时,[*]达到最小,其最小值为1/12.
解析:
[分析]: 首先要确定a与b的值,再对[*]进行讨论.
[*]
