问题
单项选择题
设4阶方阵A=[α1，α2，α3，α4]，B=[α4，α3，α2，α1]，其中α1，α2，α3，α4均为4维列向量，A可逆，且|A|=1，又设
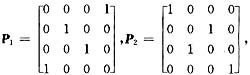则B*等于( )
答案
参考答案：C
解析：[详解] 显然矩阵B是经A的列重排后所得的矩阵，而P1是交换E的第1，4两列后所得的初等矩阵，P2是交换E的第2、3列后所得的初等矩阵，于是B=AP2P1，从而
B*=|B|B-1，
|B|=|[α4，α3，α2，α1]|=-|[α1，α3，α2，α4]|=|[α1，α2，α3，α4]
=|A|=1，
[*]
于是[*]
故应选(C)。