问题
解答题
在△ABC中，∠A，∠B，∠C所对的边分别是a，b，c．
（Ⅰ）用余弦定理证明：当∠C为钝角时，a2+b2＜c2；
（Ⅱ）当钝角△ABC的三边a，b，c是三个连续整数时，求△ABC外接圆的半径．
答案
解：（Ⅰ）当∠C为钝角时，cosC＜0，
由余弦定理得：c2=a2+b2﹣2ab
cosC＞a2+b2， 即：a2+b2＜c2．
（Ⅱ）设△ABC的三边分别为n﹣1，n，n+1（n≥2，n∈Z），
∵△ABC是钝角三角形，不妨设∠C为钝角，
由（Ⅰ）得（n﹣1）2+n2＜（n+1）2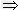
n2﹣4n＜0
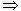0＜n＜4，
∵n≥2，n∈Z，
∴n=2，n=3，
当n=2时，不能构成三角形，舍去，
当n=3时，△ABC三边长分别为2，3，4，
，
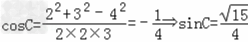△ABC外接圆的半径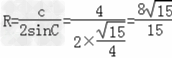
．