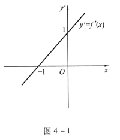
设函数y=f(x)的导函数y'=f'(x)的图像如图4-1所示,则下列结论肯定正确的是( ).
A.x=-1是驻点,但不是极值点
B.X=-1不是驻点
C.x=-1为极小值点
D.X=-1为极大值点
参考答案:C
解析:
[分析]: 本题主要考查极值的充分条件及驻点的概念.由f'(x)的图像可知,在x=-1时,f'(-1) -0,所以x=-1为驻点,排除B.而当x<-1时,f'(x)<0;x>-1时f'(x)>0.根据导数符号由负变正,可知x=-1为函数的极小值点.所以选C.
本题也可以由y'(x)的图像而得了y'=x+1,则原函数为[*]从而很容易得知选项C是正确的.
对于这种由函数导数的图像来分析和研究函数特性的方法建议考生多做练习,熟练掌握.如果本题换一种提法则可以得到另外两个选择题.
(1)设函数y=f(x)的导函数y'=f'(x)的图像如图4-1所示,则函数y=f(x)的单调递增区间为
A.(-∞,1) B.(-∞,+∞) C.(-1,+∞) D.(0,+∞) (C)
(2)设函数y=f(x)的导函数y'=f'(x)的图像如图4-1所示,则下列结论肯定正确的是
A.在(-∞,-1)内,曲线y=f(x)是凸的
B.在(-∞,+∞)内,曲线y=f(x)是凹的
C.在(-∞,+∞)内,曲线y=f(x)是凸的
D.在(-∞,+∞)内,曲线y=f(x)是直线 (B) 由于y'=x+1,则有y"=1>0,从而可以判定曲线y=f(x)在(-∞,+∞)内是凹的,所以选B
