参考答案：B

解析：

由干涉明条纹的条件知，光程差为

δ＝±Aλ(k＝0，1，2，3，…)

根据题意得，空气中(设空气的折射率n＝1.0)p点处为第三级明条纹中心，相应的光程差为：

δ＝(r₂-r₁)＝3λ (1)

将整个装置浸入某种液体中，假设透明液体的折射率为n，液体中的P点为第四级明条纹中心，则相应的光程差为：

δ＝n(r₂-r₁)＝4λ (2)

联立(1)(2)两式，解得：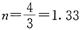

[点评] 本题是由于光路中介质变化而引起杨氏双缝干涉条纹变动的问题。已知屏幕上定点户处干涉条纹变动情况，可以得到两束相干光在该处的光程差分的变化，而光程差δ的变化与光路中引入的介质(厚度、折射率)有关，因此求解问题的关键是计算两束相干光在相遇点的光程差及其变动情况。当杨氏双缝干涉实验在空气中(设空气的折射率 n＝1.0)进行时，光程差为：δ＝(r₂-r₁)，第三级明条纹对应的光程差为：δ＝(r₂- r₁)＝3λ；当杨氏双缝干涉实验整个装置浸入某种液体中，假设透明液体的折射率为n，光程差为：δ＝n(r₂-r₁)，液体中的户点为第四级明条纹中心，则相应的光程差为：δ＝ n(r₂-r₁)＝4λ。联立求解即得正确的解答。