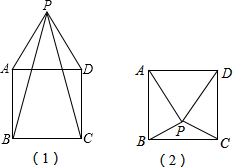
问题
填空题
已知四边形ABCD是正方形,以AD为边在正方形ABCD所在平面内作等边三角形PAD,那么∠BPC的度数是______.
答案
如图(1),
∵四边形ABCD是正方形,△PAD是等边三角形,
∴∠BAP=∠BAD+∠PAB=90°+60°=150°.
∵PA=AD,AB=AD,
∴PA=AB,
∴∠ABP=
(180°-150°)=15°,1 2
∴∠PBC=∠ABC-∠ABP=90°-15°=75°,
同理:∠PCB=75°,
∴∠BPC=180°-75°-75°=30°.
如图(2),∵四边形ABCD是正方形,△PAD是等边三角形,
∴∠BAP=∠BAD-∠PAB=90°-60°=30°.
∵PA=AD,AB=AD,
∴PA=AB,
∴∠APB=
(180°-30°)=75°,1 2
同理:∠CPD=75°,
∴∠BPC=360°-75°-75°-60°=150°.
综上可得:∠BPC的度数是30°或150°.
故答案为:30°或150°.