问题
选择题
直角梯形ABCD中，∠A=∠D=90°，DC＜AB，AB=AD=12，E是边AD上的一点，恰好使CE=10，并且∠CBE=45°，则AE的长是（ ）
A．2或8
B．4或6
C．5
D．3或7
答案
如图，过点B作BF⊥CD交DC的延长线于F，
∵∠A=∠D=90°，AB=AD，
∴四边形ABFD是正方形，
把△ABE绕点B顺时针旋转90°得到△BFG，
则AE=FG，BE=BG，∠ABE=∠FBG，
∵∠CBE=45°，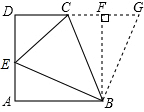
∴∠CBG=∠CBF+∠FBG=∠CBF+∠ABE=90°-∠CBE=90°-45°=45°，
∴∠CBE=∠CBG，
在△CBE和△CBG中，
，BE=BG ∠CBE=∠CBG BC=BC
∴△CBE≌△CBG（SAS），
∴CE=CG，
∴AE+CF=FG+CF=CG=CE，
设AE=x，则DE=12-x，CF=10-x，
∴CD=12-（10-x）=x+2，
在Rt△CDE中，CD2+DE2=CE2，
即（x+2）2+（12-x）2=102，
整理得，x2-10x+24=0，
解得x1=4，x2=6，
所以AE的长是4或6．
故选B．
