问题
证明题
同一底上的两底角相等的梯形是等腰梯形吗?如果是,请给出证明(要求画出图形,写出已知、求证、证明);如果不是,请给出反例(只需画图说明)
答案
| 是等腰梯形 |
| 已知:梯形ABCD,AD∥BC且∠B=∠C(或∠A=∠D) |
| 求证:梯形ABCD是等腰梯形 |
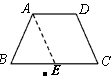
| 证明一:过点A作AE∥DC,交BC于E |
| ∵AD∥BC AE∥DC ∴四边形AECD是平行四边形, |
| ∴∠AEB=∠C, AE=DC |
| ∵∠B=∠C ∴∠AEB=∠B ∴AB=AE ∴AB=DC |
| ∴梯形ABCD是等腰梯形 |
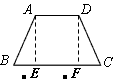
| 证明二:过A、D两点分别作AE⊥BC,DF⊥BC垂足为E、F |
| ∵AE⊥BC、DF⊥BC ∴AE∥DF且∠AEB=∠DFC |
| ∵AD∥BC ∴四边形AEFD是平行四边形 |
∴AE=DF ∵∠AEB=∠DFC ∠B=∠C
∴△AEB≌△DFC ∴AB=DC
∴梯形ABCD是等腰梯形
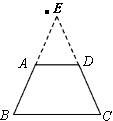
证明三:延长BA、CD交于E点
∵∠B=∠C ∴BE=CE ∴AD∥BC ∴∠EAD=∠B,∠EDA=∠C
∴∠EAD=∠EDA ∴AE=DE ∴AB=DC
∴梯形ABCD是等腰梯形