问题
解答题
已知△ABC的一边为5,另外两边恰是方程x2-6x+m=0的两个根.
(1)求实数m的取值范围.
(2)当m取最大值时,求△ABC的面积.
答案
(1)设另两边为x1,x2,且x1>x2.
∴由韦达定理,得
x1+x2=6,x1•x2,=m;
根据三边关系得:
x1+x2=6>5①;
∴x1-x2=
=(x1+x2)2-4x1x2
<5;36-4m 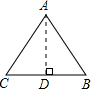
解得,m>
;11 2
又∵△=36-4m≥0,
解得,m≤9,
∴m的取值范围是:
<m≤9;11 2
(2)当m取最大值,即m=9时,由原方程得
x2-6x+9=0,即(x-3)2=0,
解得,x1=x2=3,
过点A作AD⊥BC于点D.
∴AD=11 2
∴S△ABC=
.5 11 4
