解：已知：梯形ABCD 中，AD//BC，BC>AD，E、F分别为对角线BD、AC的中点，求证：EF//AD//BC，且EF=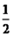 (BC-AD).

证明：延长EF交CD与N，延长FE交AB于M，连接DF并延长交BC于G.

∵AD//BC,

∴∠DAF=∠FCG，∠ADF=∠CGF.

又AF= CF,

∴△ADF≌△CGF.

∴DF=GF.

∵E是BD的中点.

∴EF为△DBG的中位线.

∴EF//BG，又AD//BC

∴EF//AD//BC.

∴E、F分别是BD、AC的中点，且EF//AD//BC.

∴MN为梯形ABCD的中位线，MN=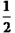(AD+BC).

又ME=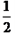AD= FN.

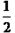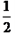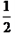∴EF= MN-MB-FN=(AD+BC)-AD-AD= 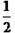(BC-AD).

∴梯形对角线中点的连线平行于两底. 并且等于两底差的一半。