问题
解答题
已知关于x的方程x2+mx+n=0的根为2和-2，求x2+nx+m=0的两根。
答案
解：∵x的方程x2+mx+n=0的根为2和-2
∴
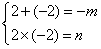解得
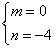
∴ x2-4x=0，解得x1=0，x2=4
故x2+nx+m=0的两根为x1=0，x2=4。
搜题请搜索小程序“爱下问搜题”
已知关于x的方程x2+mx+n=0的根为2和-2，求x2+nx+m=0的两根。
解：∵x的方程x2+mx+n=0的根为2和-2
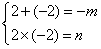∴ 解得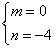
∴ x2-4x=0，解得x1=0，x2=4
故x2+nx+m=0的两根为x1=0，x2=4。