问题
解答题
求椭圆25x2+y2=25的长轴和短轴的长、焦点和顶点坐标及离心率.
答案
椭圆的离心率是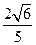
把已知方程化成标准方程: 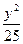 +x2=1,
+x2=1,
这里a=5,b=1,所以c=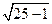 =2
=2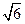 .
.
因此,椭圆的长轴和短轴的长分别是2a=10和2b=2,两个焦点分别是F1(0,-2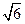 )、F2(0,2
)、F2(0,2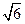 ),椭圆的四个顶点是A1(0,-5)、A2(0,5)、B1(-1,0)和B2(1,0),椭圆的离心率是
),椭圆的四个顶点是A1(0,-5)、A2(0,5)、B1(-1,0)和B2(1,0),椭圆的离心率是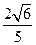 .
.
求椭圆25x2+y2=25的长轴和短轴的长、焦点和顶点坐标及离心率.
椭圆的离心率是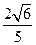
把已知方程化成标准方程: 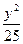 +x2=1,
+x2=1,
这里a=5,b=1,所以c=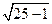 =2
=2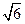 .
.
因此,椭圆的长轴和短轴的长分别是2a=10和2b=2,两个焦点分别是F1(0,-2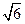 )、F2(0,2
)、F2(0,2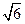 ),椭圆的四个顶点是A1(0,-5)、A2(0,5)、B1(-1,0)和B2(1,0),椭圆的离心率是
),椭圆的四个顶点是A1(0,-5)、A2(0,5)、B1(-1,0)和B2(1,0),椭圆的离心率是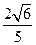 .
.