问题
单项选择题
在图4-2中,由点O(0,0)到点P(5,6)的最短路径共有 (39) 条。
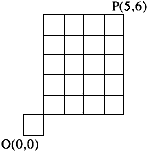
图4-2 求最短路径
答案
参考答案:C
解析:[要点解析] 图4-2中点O到点P的最短路径,即只能向上或向右走的所有路径。可以分两步来求从点O到点P的最短路径:
1) 从O到点(1,1):共2条路径,分别是光向上和先向右走。
2) 从点(1,1)到点P:设向右走一格的长度为J,向上走一格的长度为y,那么不管怎么走,从点(1,1)出发,总是要经过4个x,5个y,方能到达点P,所以一条从点(1,1)到点P的最短路径对应一个由4个x、 5个y共9个元素构成的排列;反之,给定一个这样的排列,按照x,y的含义,必对应一条从点(1,1)到点 P的最短路径。故从点(1,1)到点P的最短路径计算转换为相异元素的全排列问题,其解为从排列的9个位置中选出4个位置放x,剩下的5个位置放y,计数结果为[*]。
按照乘法规则,从点O到点P的最短路径数为2×126=252条。
