问题
单项选择题
设y=g(x)由方程y=f(x2+y2)+f(x+y)确定，且y(0)=2，其中f(x)是可导函数，且
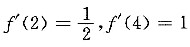，则y'(0)等于
答案
参考答案：B
解析：[详解] 方程y=f(x2+y2)+f(x+y)的两边对x求导，得
y'=f'(x2+y2)(2x+2yy')+f'(x+y)(1+y')．
令x=0，得
y'(0)=f'(22)(2×0+2×2y'(0))+f'(2)(1+y'(0))．
于是y'(0)=4y'(0)f'(4)+f'(2)(1+y'(0))．
因为[*]，所以
[*]
则有[*]，故应选(B)．