问题
解答题
设△ABC的三边BC=4pq,CA=3p2+q2,AB=3p2+2pq-q2,求∠B,并证∠B为∠A及∠C的等差中项.
答案
由余弦定理可得:
cosB=
=AB2+BC2-CA2 2AB•BC (3p2+2pq-q2) 2+(4pq)2-(3p2+q2) 2 2(3p2+2pq-q2)• 4pq
=
=4pq(3p2+2pq-q2) 8pq(3p2+2pq-q2)
,1 2
∴∠B=60°,
∵∠C-∠B=(180°-∠A-∠B)-∠B=60°-∠A
=∠B-∠A,
∴∠B是∠A与∠C的等差中项.

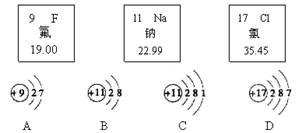
 )与B(
)与B( )反应生成C(
)反应生成C( ),下图是其反应前后分子及其数目变化的微观示意图(“
),下图是其反应前后分子及其数目变化的微观示意图(“ ”和“
”和“ ”分别表示碳原子和氧原子),若要与0.2L的A恰好完全反应,所需B的体积为 。
”分别表示碳原子和氧原子),若要与0.2L的A恰好完全反应,所需B的体积为 。