问题
填空题
已知椭圆的焦点是F1(-1,0)、F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|与|PF2|的等差中项,则椭圆方程为_________________.
答案
+
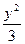=1
∵|F1F2|=2,∴|PF1|+|PF2|=2|F1F2|=4,即2a=4.
∴a=2.又c=1,∴b2=3.
而椭圆焦点在x轴上,
∴所求椭圆方程为+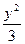=1.
搜题请搜索小程序“爱下问搜题”
已知椭圆的焦点是F1(-1,0)、F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|与|PF2|的等差中项,则椭圆方程为_________________.
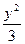+=1
∵|F1F2|=2,∴|PF1|+|PF2|=2|F1F2|=4,即2a=4.
∴a=2.又c=1,∴b2=3.
而椭圆焦点在x轴上,
∴所求椭圆方程为+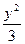=1.