问题
计算题
用适当的方法解下列方程
|
答案
（1）
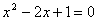配方，得（x-1）2=0
∴x-1=0
因此，x1=x2=1
移项，得x2+2x=3
配方，得x2+2x+1=3+1 即 (x+1)2=4
开方，得x+1=±2 所以，x1=1，x2=-3
（3）
这里a=2，b=5，c=-1
∴b2-4ac=52-4×2×(-1)=33
∴
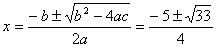
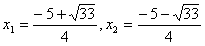
∴2(x-3)2=（x+3）(x-3)
∴2(x-3)2-（x+3）(x-3)=0
∴(x-3)[2(x-3)-(x+3)]=0
∴x-3=0 2(x-3)-(x+3)=0
所以x1=3, x2=9
填空题
| 选择正确的词填空。 | |
| |
| 1. I ______ a student. My name ______ Li Hong. 2. She ______ my friend. Her name ______ Wang Mei. 3. Where ______ your balls? They ______ under the bed. 4. ______ those apples? Yes, they ______. 5. On Sunday, I ______ watch TV. I must do my homework. 6. ______ her daughter have a nice English name? - Yes, she does. 7. ______ you spell the word? - Sorry, I can't 8. ______ his grandparents like him? 9. —Where ______ I? —You ______ in a new place. 10. —What ______ your uncle love? —He loves sports. |