问题
解答题
已知椭圆的两焦点为F1(0，－1)、F2(0，1)，直线y=4是椭圆的一条准线.
(1)求椭圆方程；
(2)设点P在椭圆上，且|PF1|－|PF2|=1，求tan∠F1PF2的值.
答案
(1) 椭圆方程为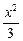
+
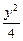=1.
(2) 
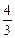
本题考查椭圆的基本性质及解题的综合能力.
(1)设椭圆方程为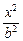
+
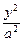=1(a>b>0).
由题设知c=1，
=4,∴a2=4,b2=a2－c2=3.
∴所求椭圆方程为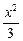+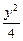=1.
(2)由(1)知a2=4,a=2.
由椭圆定义知|PF1|+|PF2|=4，又|PF1|－|PF2|=1,
∴|PF1|=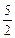
，|PF2|=
.
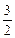又|F1F2|=2c=2,
由余弦定理cos∠F1PF2=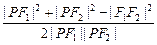
=
=
.
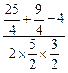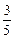∴tan∠F1PF2=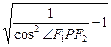
=
=.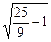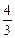