问题
解答题
已知一动圆M,恒过点F(1,0),且总与直线l:x=﹣1相切.
(1)求动圆圆心M的轨迹C的方程;
(2)探究在曲线C上,是否存在异于原点的A(x1,y1),B(x2,y2)两点,当y1y2=﹣16时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
答案
解:(1)因为动圆M,过点F(1,0)且与直线l:x=﹣1相切,
所以圆心M到F的距离等于到直线l的距离.
所以,点M的轨迹是以F为焦点,l为准线的抛物线,且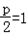 ,p=2,
,p=2,
所以所求的轨迹方程为y2=4x
(2)假设存在A,B在y2=4x上,
所以,直线AB的方程: ,
,
即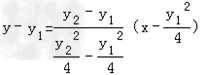
即AB的方程为: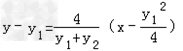 ,
,
即(y1+y2)y﹣y12﹣y1y2=4x﹣y12
即:(y1+y2)y+(16﹣4x)=0,
令y=0,得x=4,所以,无论y1,y2为何值,直线AB过定点(4,0)
