动圆圆心的轨迹方程为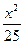+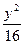=1.

已知圆方程配方整理得(x+3)²+y²=10²,圆心为C₁(-3,0),半径为R=10.

设所求动圆圆心为C(x,y),半径为r,依题意有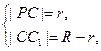

消去r得R-|PC|=|CC₁|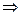|PC|+|CC₁|=R,

即|PC|+|CC₁|=10.

又P(3,0)、C₁(-3,0),且|PC₁|=6<10,

可见C点是以P、C₁为两焦点的椭圆,且c=3,2a=10.

∴a=5,从而b=4.故所求的动圆圆心的轨迹方程为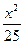+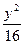=1.