问题
单项选择题
设偶函数f(x)的二阶导数f"(x)在x=0的某一个邻域内连续,且f(0)=1,f"(0)=2,则级数
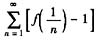
答案
参考答案:B
解析:
[分析]: 由于f(x)为偶函数,可知f(-x)=f(x),又由f(x)在x=0的某邻域内有二阶连续导数,可知在该邻域f'(x)为奇函数(f'(x)=-f'(-z)),从而知f'(0)=0,又由题设f"(0)=2可知x=0为f(x)的极小值点,由于f(0)=1,则在x=0的某邻域内必有f(x)>1,因此存在N>0,当n>N时,总有[*]为正项级数。
考察两个正项级数[*]由题设条件及上述推导,可得
[*]
取[*]可知[*]收敛,由正项级数极限形式的比较判别法知[*]收敛,进而可知[*]收敛,且为绝对收敛,因此选(B)。
[*]

