问题
单项选择题
设f(x)在[1,+∞)内可导,则下列结论中成立的是
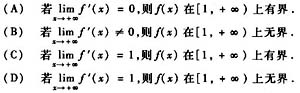
答案
参考答案:D
解析:
[分析]: 首先举例说明(A),(B)皆错,设[*]则
[*]但是[*]上无界,故(A)不成立。
又设f(x)=sinx,则
[*]
[*]但是sinx在[1,+∞)上为有界函数,故(B)也不成立。
下面讨论(C)或(D),假设f(x)在[1,+∞)上有界,则[*]M>0,使得[*]∈[1,+∞)有|f(x)|≤M。在区间[x,2x]上应用拉格朗日中值定理即知存在ξ∈(x,2x),使得
f(2x)-f(x)=f'(ξ)(2x-x)=f'(ξ)x
令x→+∞,上式左边
|f(2x)-f(x)|≤|f(2x)|+|f(x)|≤2M;
而右边因x→+∞时ξ→+∞,所以
[*]
从而导出了矛盾,这表明f(x)在[1,+∞)上无界,即(C)不成立,故选(D)。
[*]
