问题
解答题
已知△ABC的周长为12，顶点A，B的坐标分别为(－2,0)，(2,0)，C为动点．
(1)求动点C的轨迹E的方程；
(2)过原点作两条关于y轴对称的直线(不与坐标轴重合)，使它们分别与曲线E交于两点，求四点所对应的四边形的面积的最大值．
答案
（1）
＋
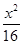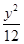＝1(x≠±4)
（2）16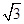
(1)由题意知|CA|＋|CB|＝12－4＝8>|AB|，所以C的轨迹E为椭圆的一部分．
由a＝4，c＝2，可得b2＝12．
故曲线E的方程为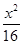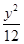＋＝1(x≠±4)．
(2)设两直线的方程为y＝kx与y＝－kx(k>0)．记y＝kx与曲线E在第一象限内的交点为(x0，y0)，由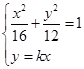
，可得x02＝
．
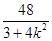结合图形的对称性可知：四交点对应的四边形为矩形，且其面积S＝2x0·2y0＝4kx02＝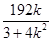
．
因为k>0，所以S＝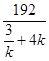
≤
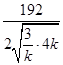＝16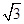 (当且仅当k＝
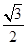时取等号)．故四边形面积的最大值为16．
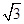